Comment fonctionne un code à barres?

Salut à tous! 

De nos jours, chaque personne utilise des codes à barres, la plupart du temps sans s'en rendre compte. Lorsque nous achetons des produits d'épicerie dans le magasin, leurs identifiants proviennent de codes à barres. Il en va de même pour les marchandises dans les entrepôts, les colis postaux, etc. Mais peu de gens savent réellement comment cela fonctionne. 

Qu'est-ce que "l'intérieur" du code à barres et qu'est-ce qui est encodé sur cette image? 



Permet de comprendre, et permet également d'écrire notre propre décodeur de barre.

introduction

L'utilisation de codes à barres a une longue histoire. Les premières tentatives d'automatisation ont été faites dans les années 50, le brevet pour un système de lecture de codes a été accordé. David Collins, qui travaillait au Pennsylvania Railroad, a décidé de faciliter le processus de tri des voitures. L'idée était évidente: coder les identifiants de voiture avec différentes bandes de couleur et les lire à l'aide d'une cellule photoélectrique. En 1962, de tels codes sont devenus une norme de l’Association of American Railroads. (le KarTraksystème). En 1968, la lampe a été remplacée par un laser, ce qui a permis d’augmenter la précision et de réduire la taille du lecteur. Le code universel des produits a été mis au point en 1973 et, en 1974, le premier produit d’épicerie (un chewing-gum de Wrigley, c’est évidemment aux États-Unis;) a été vendu. En 1984, la troisième partie de tous les magasins utilisaient des codes à barres, dans d'autres pays, il est devenu populaire plus tard. 

Il existe de nombreux types de codes à barres pour différentes applications. Par exemple, la chaîne «12345678» peut être codée de cette manière (et non la totalité): 



Permet de lancer l'analyse. Toutes les informations ci-dessous concernent le type «Code-128» - simplement parce qu’il est facile à comprendre le principe. Ceux qui souhaitent tester d’autres modes peuvent utiliser le générateur de codes à barres en ligne et en tester d’autres.

À première vue, un code à barres ressemble à un ensemble aléatoire de chiffres, mais sa structure est en fait bien organisée: 



1 - Espace vide, nécessaire pour déterminer la position de départ du code. 
2 - Symbole de départ. Trois types de Code-128 sont disponibles (appelés A, B et C) et les symboles de début peuvent être 11010000100, 11010010000 ou 11010011100 respectivement. Pour ces types, les tables de codage sont différentes (voir la description de Code_128 pour plus de détails ). 
3 - Le code lui-même, contenant les données de l'utilisateur. 
4 - Somme de contrôle. 
5 - Symbole d'arrêt, pour Code-128 et son 1100011101011. 
6 (1) - Espace vide.

Voyons maintenant comment les bits sont codés. C'est vraiment facile - si nous prenons la largeur de ligne la plus fine à «1», alors la ligne à double largeur sera «11», la ligne à triple largeur est «111», etc. L'espace vide sera respectivement «0», «00» ou «000», selon le même principe. Ceux qui sont intéressés peuvent comparer la séquence de départ sur l'image ci-dessus pour vérifier que la règle est respectée. 

Nous pouvons maintenant commencer à coder.

Obtenir la séquence de bits

En général, c'est la partie la plus compliquée, et cela peut se faire de différentes manières. Je ne suis pas sûr que mon approche soit optimale, mais pour notre tâche, cela suffit. 

Premièrement, permet de charger l’image, d’étirer sa largeur, de couper une ligne horizontale à partir du milieu, de la convertir en couleur n / b et de l’enregistrer sous forme de tableau.

from PIL import Image
import numpy as np
import matplotlib.pyplot as plt

image_path = "barcode.jpg"
img = Image.open(image_path)
width, height = img.size
basewidth = 4*width
img = img.resize((basewidth, height), Image.ANTIALIAS)
hor_line_bw = img.crop((0, int(height/2), basewidth, int(height/2) + 1)).convert('L')
hor_data = np.asarray(hor_line_bw, dtype="int32")[0]

Sur le code à barres, la ligne noire correspond à «1», mais en RVB le noir est au contraire à 0, le tableau doit donc être inversé. Nous allons également calculer la valeur moyenne.

hor_data = 255 - hor_data
avg = np.average(hor_data)

plt.plot(hor_data)
plt.show()

Lançons le programme pour vérifier que le code à barres a été correctement chargé: 



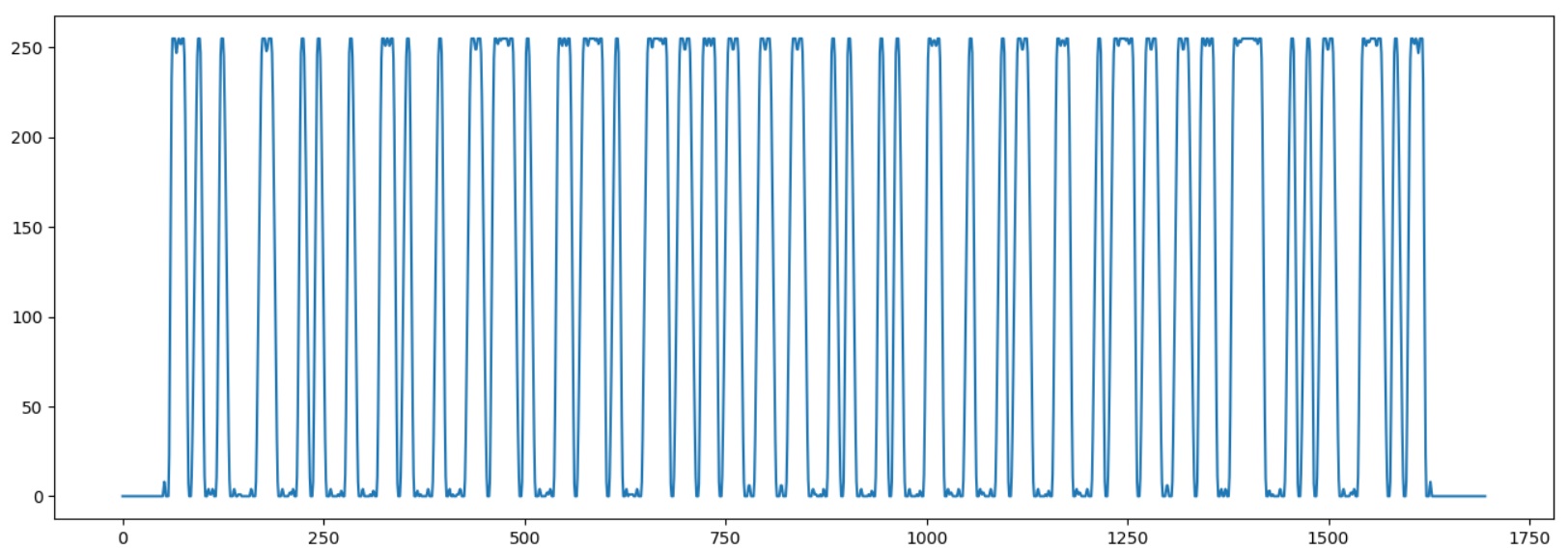
Maintenant, nous devons déterminer une largeur d'un bit. Pour ce faire, nous allons extraire la séquence en sauvegardant les positions du croisement moyen des lignes.

pos1, pos2 = -1, -1
bits = ""
for p in range(basewidth - 2):
    if hor_data[p] < avg and hor_data[p + 1] > avg:
        bits += "1"
        if pos1 == -1:
            pos1 = p
        if bits == "101":
            pos2 = p
            break
    if hor_data[p] > avg and hor_data[p + 1] < avg:
        bits += "0"

bit_width = int((pos2 - pos1)/3)

Nous enregistrons uniquement le nombre moyen de croisements de lignes, le code «1101» sera donc enregistré sous le numéro «101», mais sa largeur en pixels est suffisante. 

Maintenant, faisons le décodage lui-même. Nous devons trouver chaque ligne moyenne traversant et trouver le nombre de bits dans le dernier intervalle trouvé. Les nombres ne correspondront pas parfaitement (le code peut être étiré ou plié un peu), nous devons donc arrondir la valeur à un entier.

bits = ""
for p in range(basewidth - 2):
    if hor_data[p] > avg and hor_data[p + 1] < avg:
        interval = p - pos1
        cnt = interval/bit_width
        bits += "1"*int(round(cnt))
        pos1 = p
    if hor_data[p] < avg and hor_data[p + 1] > avg:
        interval = p - pos1
        cnt = interval/bit_width
        bits += "0"*int(round(cnt))
        pos1 = p

Peut-être y a-t-il une meilleure façon de faire cela, les lecteurs peuvent écrire des commentaires. 

Si tout était parfait, nous aurions une séquence comme celle-ci:

11010010000110001010001000110100010001101110100011011101000111011011
01100110011000101000101000110001000101100011000101110110011011001111
00010101100011101011

Décodage

En général, c'est assez facile. Les symboles du Code-128 sont codés avec un code de 11 bits pouvant avoir un codage différent (selon ce codage - A, B ou С, il peut s'agir de lettres ou de chiffres de 00 à 99). 

Dans notre cas, le début de la séquence est 11010010000, ce qui correspond à un «Code B». J'étais trop paresseux pour entrer tous les codes manuellement, alors je l'ai simplement copié-collé depuis une page Wikipedia. L'analyse de ces lignes a également été effectuée sur Python (astuce - ne faites pas de telles choses en production).

    CODE128_CHART = """
        0 _ _ 00 32 S 11011001100 212222
        1 ! ! 01 33 ! 11001101100 222122
        2 " " 02 34 " 11001100110 222221
        3 # # 03 35 # 10010011000 121223
        ...
        93 GS } 93 125 } 10100011110 111341
        94 RS ~ 94 126 ~ 10001011110 131141
        103 Start Start A 208 SCA 11010000100 211412
        104 Start Start B 209 SCB 11010010000 211214
        105 Start Start C 210 SCC 11010011100 211232
        106 Stop Stop - - - 11000111010 233111""".split()
    SYMBOLS = [value for value in CODE128_CHART[6::8]]
    VALUESB = [value for value in CODE128_CHART[2::8]]
    CODE128B = dict(zip(SYMBOLS, VALUESB))

Les dernières parties sont faciles. Commençons par diviser la séquence en blocs de 11 bits:

sym_len = 11
symbols = [bits[i:i+sym_len] for i in range(0, len(bits), sym_len)]

Enfin, générons la chaîne de sortie et l’affiche:

str_out = ""
for sym in symbols:
    if CODE128A[sym] == 'Start':
        continue
    if CODE128A[sym] == 'Stop':
        break
    str_out += CODE128A[sym]
    print("  ", sym, CODE128A[sym])

print("Str:", str_out)

Je ne vais pas montrer ici le résultat décodé de l'image du haut, mais que ce soit le devoir des lecteurs (utiliser les applications téléchargées pour les smartphones sera considéré comme de la triche :). 

Le contrôle CRC n’est pas implémenté dans ce code, ceux qui le souhaitent peuvent le faire eux-mêmes. 

Bien sûr, cet algorithme n'est pas parfait, cela a été fait en une demi-heure. Pour les tâches professionnelles, il existe des bibliothèques prêtes à l’emploi, par exemple pyzbar . Pour décoder l’image, 4 lignes de code suffisent:

from pyzbar.pyzbar import decode

img = Image.open(image_path)
decode = decode(img)
print(decode)

(la bibliothèque doit d'abord être installée à l'aide de la commande «pip install pyzbar») 

Ajout : l'utilisateur du site vinograd19 a envoyé un commentaire intéressant sur l'historique de calcul de la somme de contrôle des codes à barres. 

Le calcul du nombre de chèques est intéressant, il est né de façon évolutive. 
La somme de contrôle est évidemment nécessaire pour éviter un décodage erroné. Si le code à barres était 1234 et qu'il était décodé en tant que 7234, nous avons besoin d'une méthode pour refuser de remplacer 1 à 7. La validation peut ne pas être parfaite, mais au moins 90% des codes doivent être vérifiés correctement.

1ère approche: prenons simplement la somme, pour avoir 0 comme reste de la division. Les premiers symboles contiennent des données, et le dernier chiffre est choisi, de sorte que la somme de tous les nombres soit divisée par 10. Après le décodage, si le montant n'est pas divisible par 10, le décodage est incorrect et doit être répété. Par exemple, le code 1234 est valide - 1 + 2 + 3 + 4 = 10. Le code 1216 - est également valide, mais 1218 ne l’est pas.

Cela aide à éviter les problèmes de décodage. Mais les codes peuvent également être saisis manuellement, à l'aide du clavier matériel. En utilisant ceci, un autre mauvais cas a été trouvé - si l'ordre des deux chiffres sera changé, la somme de contrôle sera toujours correcte, c'est définitivement mauvais. Par exemple, si le code à barres 1234 a été saisi en tant que 2134, la somme de contrôle sera la même. Il a été constaté qu’un ordre incorrect de chiffres était le cas courant si une personne essayait d’entrer rapidement les chiffres.

2ème approche. Permet d'améliorer l'algorithme de la somme de contrôle - permet de calculer les nombres impairs deux fois. Ensuite, si la commande est modifiée, la somme sera incorrecte. Par exemple, le code 2364 est valide (2 + 3 * 2 + 6 + 4 * 2 = 20), mais le code 3264 n'est pas (3 + 2 * 2 + 6 + 4 * 2 = 19). C'est mieux, mais un autre cas est apparu. Certains claviers ont 10 touches sur deux lignes, la première ligne est 12345 et la seconde 67890. Si au lieu de «1», l'utilisateur saisit «2», la vérification de la somme de contrôle échouera. Mais si l'utilisateur doit entrer «6» au lieu de «1», la somme de contrôle peut être parfois correcte. C'est parce que 6 = 1 + 5, et si le chiffre a une place impaire, nous obtenons 2 * 6 = 2 * 1 + 2 * 5 - la somme a été augmentée de 10. La même erreur se produira si l'utilisateur saisit «7 »Au lieu de« 2 »,« 8 »au lieu de« 3 », etc.

3ème approche. Reprenons la somme, mais obtenons des nombres impairs… 3 fois. Par exemple, le code 1234565 - est valide, car 1 + 2 * 3 + 3 + 4 * 3 + 5 + 6 * 3 +5 = 50. 

Cette méthode est devenue une norme pour le code EAN13, avec quelques modifications: le nombre de chiffres est fixe et égal à 13, où 13ème chiffre - est la somme de contrôle. Les nombres aux endroits impairs sont comptés trois fois, aux endroits pairs une fois. 

À propos, le code EAN-13 est le plus utilisé dans les centres commerciaux et les centres commerciaux. Il est donc plus fréquent que les autres types de code. Son codage en bits est le même que dans Code-128, la structure de données peut être trouvée dans l'article Wikipedia .

Conclusion

Comme nous pouvons le constater, même une chose aussi simple qu'un code à barres peut contenir des éléments intéressants. À propos, un autre petit bouleversement pour les lecteurs, qui ont eu la patience de lire jusqu’à cet endroit - le texte sous le code à barres est totalement identique aux données du code à barres. Il a été conçu pour les opérateurs, qui peuvent saisir manuellement le code s’il n’est pas lisible par le scanner. Il est donc facile de connaître le contenu du code à barres - il suffit de lire le texte ci-dessous. 

Merci d'avoir lu.

Astuceinformatique

Partager :